Gli algoritmi di ottimizzazione svolgono un ruolo cruciale nel trovare i parametri ottimali di un modello, ==con l’obiettivo aggiornare i parametri del modello rappresentati da (pesi) e (bias) al fine di ridurre al minimo una funzione di perdita che misura la discrepanza tra le previsioni del modello e i dati reali==.
A partire da dei pesi assegnati casuialmente, ad ogni iterazione della rete (epoca) viene chiamato l’algoritmo in questione al fine di aggiustare i pesi e convergere al minimo della loss function.
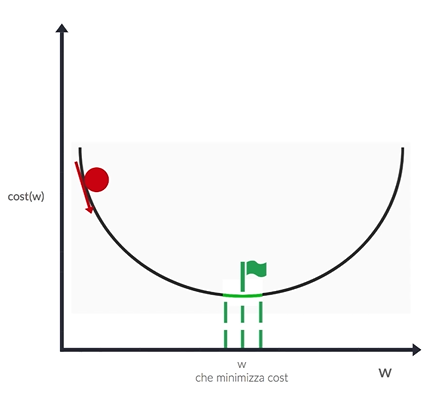
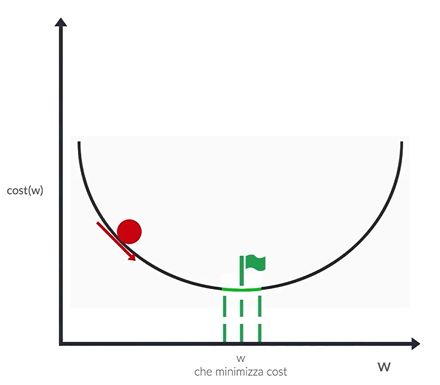
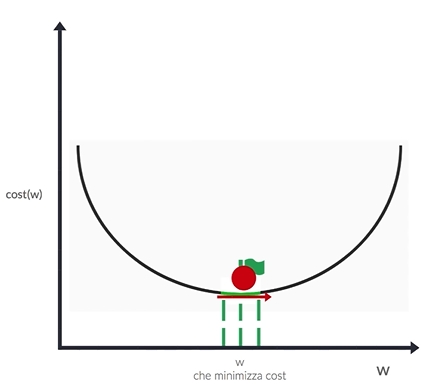
Gli algoritmi di ottimizzazione possono essere suddivisi in diverse categorie, ognuna con le proprie caratteristiche e applicazioni. Le categorie principali includono:
Gradient Descent
Gli algoritmi di discesa del gradiente (Gradient Descent) utilizzano il gradiente della funzione di costo rispetto ai parametri del modello per aggiornare iterativamente i pesi e i bias al fine di ridurre la loss.
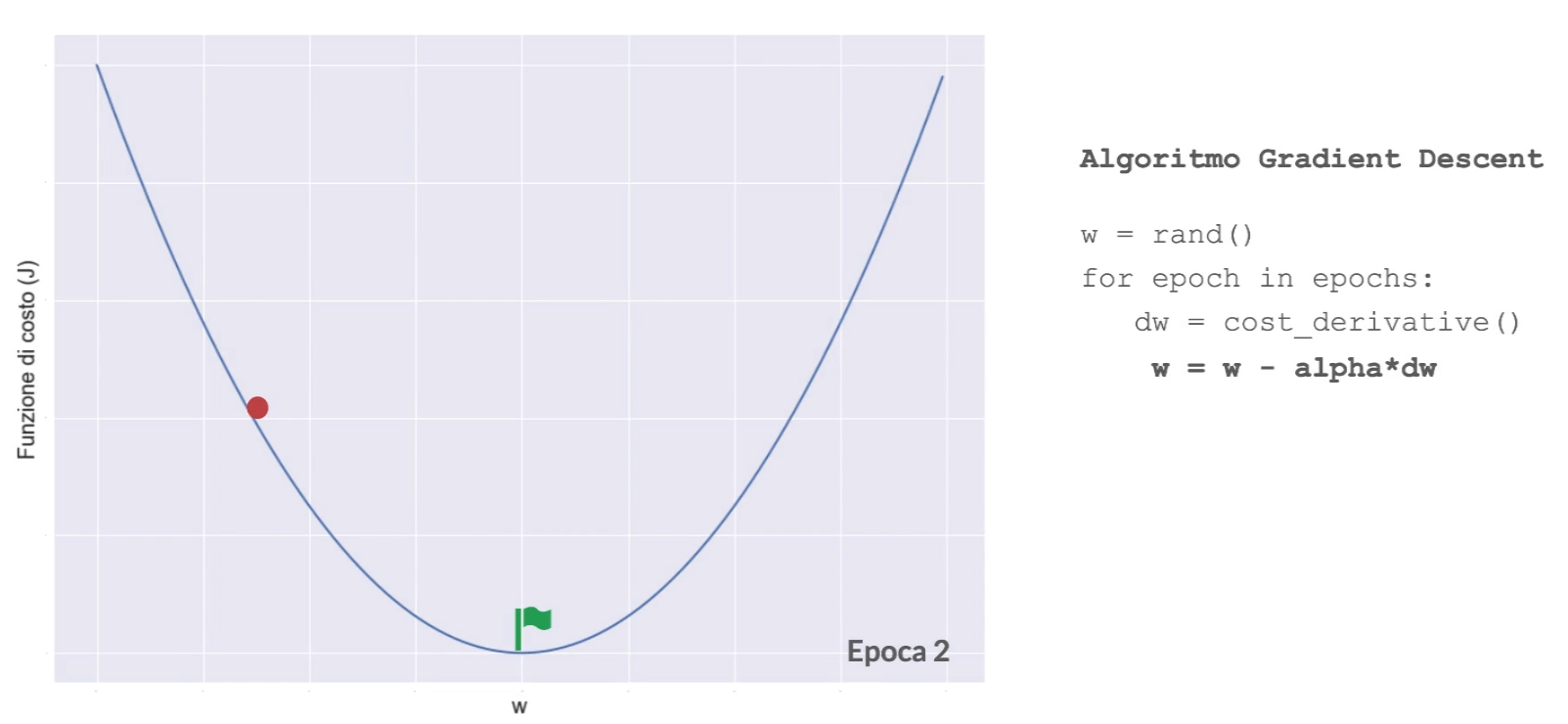
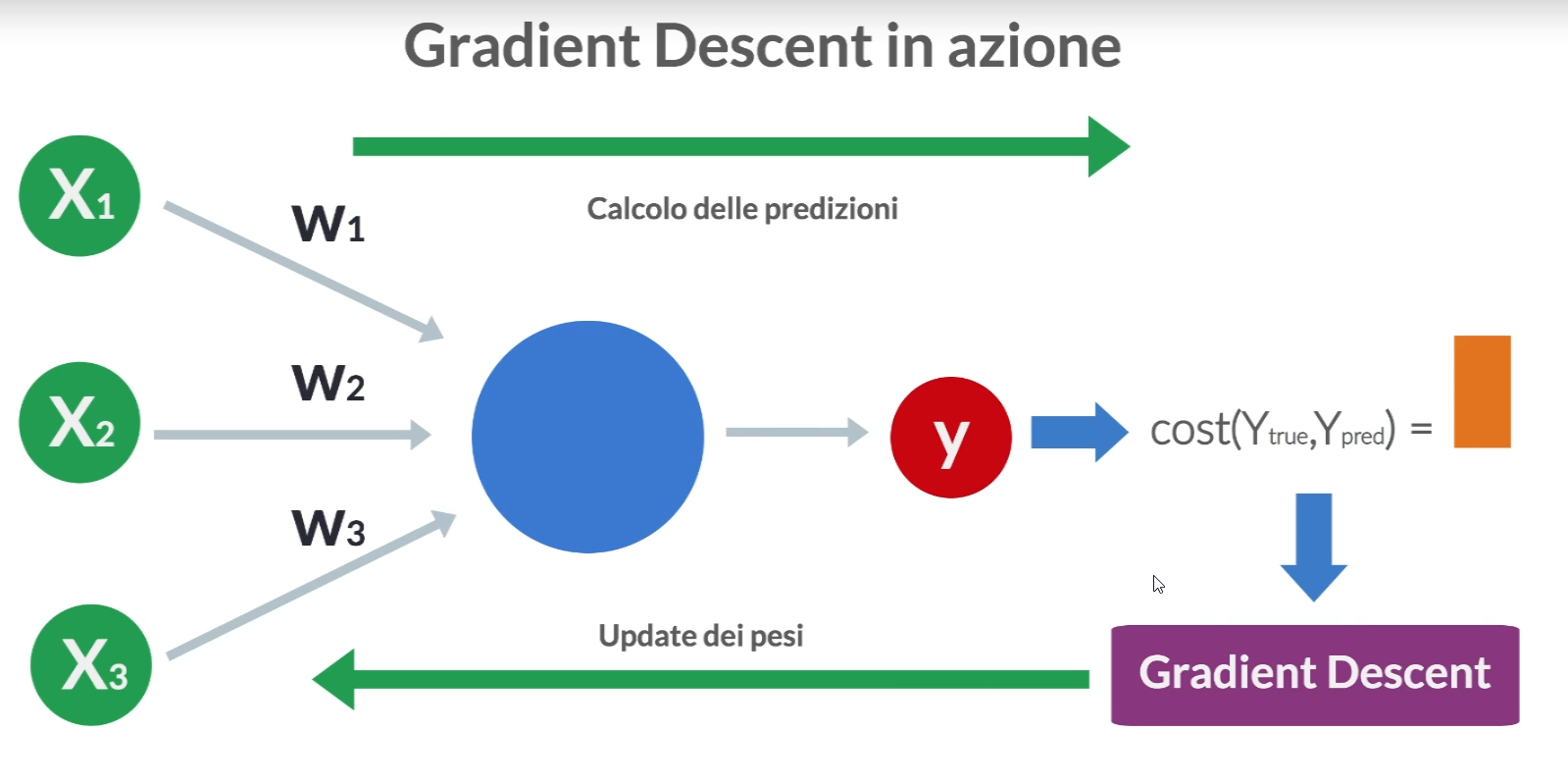
Full Batch Gradient Descent
Con questo algoritmo tutti gli esempi del set di addestramento vengono utilizzati per eseguire un singolo step del gradient descent e aggiornare i pesi.
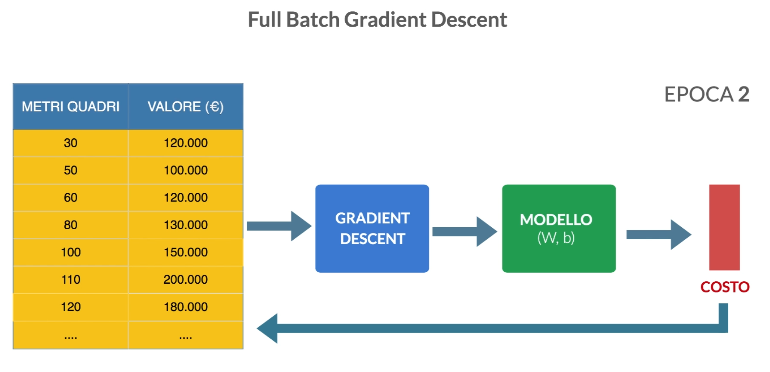
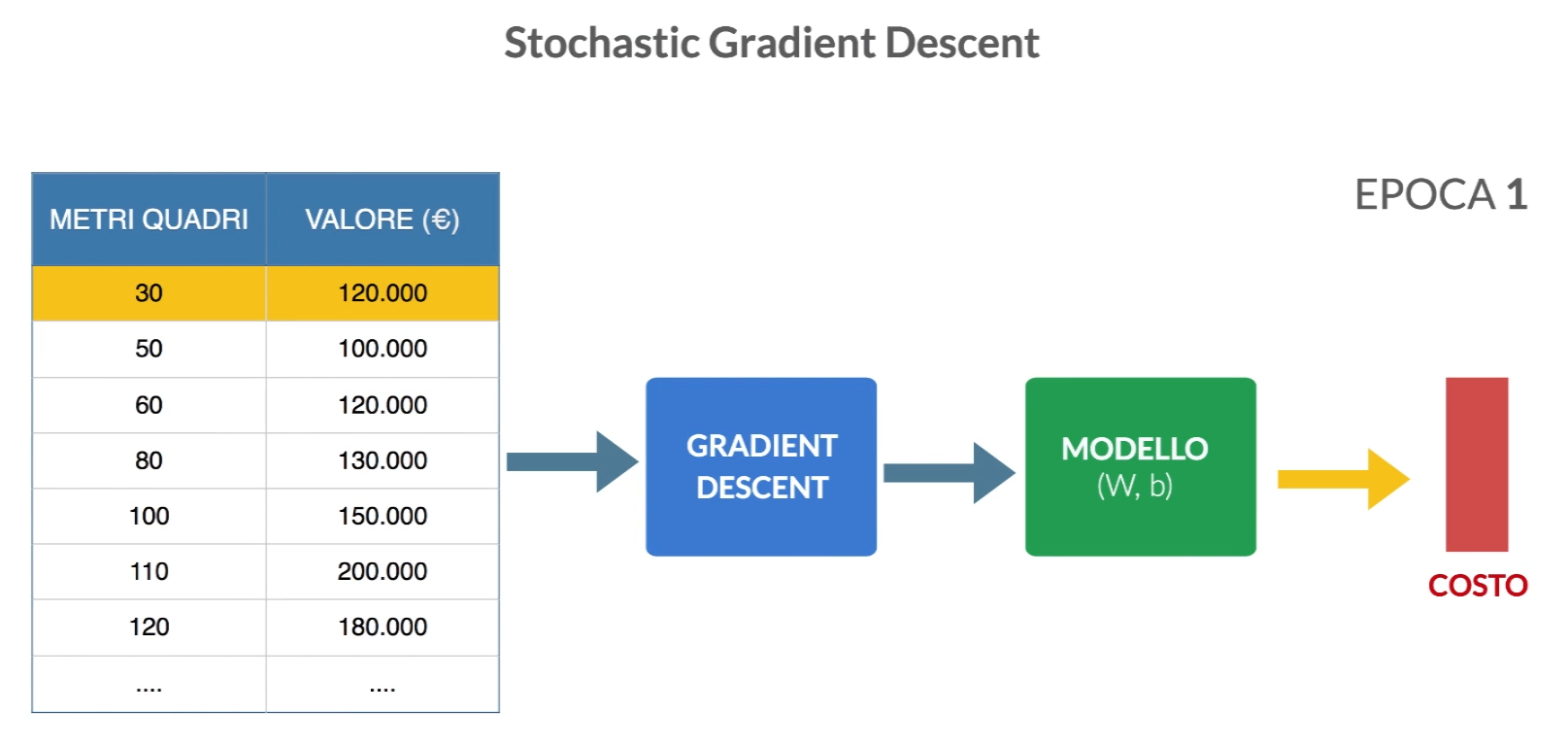
Stochastic Gradient Descent
Con questo algoritmo il gradient descent viene chiamato n volte con ogni volta in ingresso una sola riga del dataset. gli esempi del set di addestramento vengono utilizzati per eseguire un singolo step del gradient descent e aggiornare i pesi. In questo caso è probabile che la funzione di costo oscilli in quanto sto chiamando ‘ottimizzatore con una sola riga per volta. All’epoca successiva rimescolerò i dati di addestramento in modo casuale in modo che fornisce all’ottimizzatore dati con ordine sempre diverso.
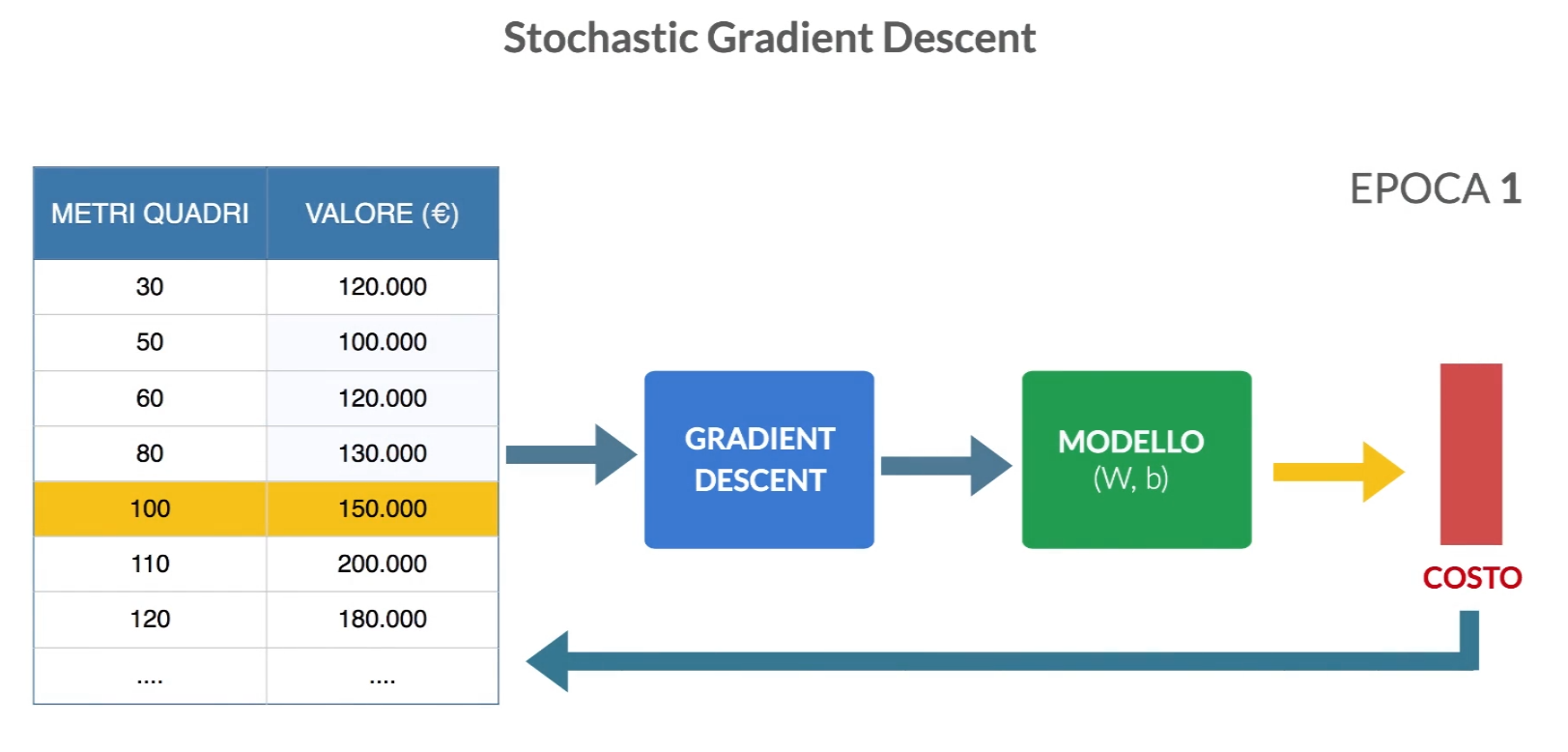
Mini Batch Gradient Descent
Questo algorimo esegue il gradient descent su un numero determinato di esempi di training set per volta.
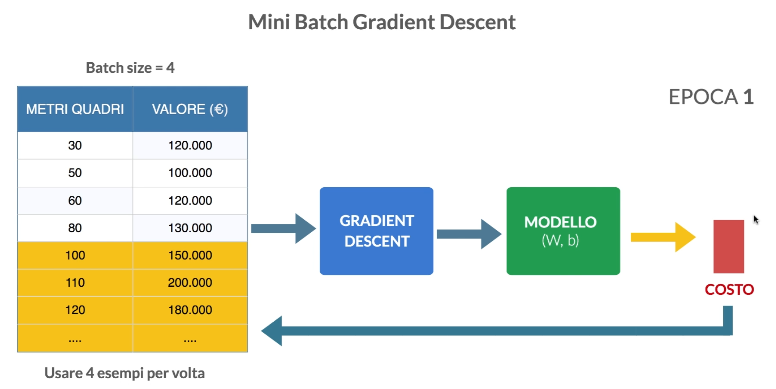Questo è l’algoritmo migliore. I valori consigliati di batch size sono 32, 64, 128, 256 e 512.
Per approfondire vedi la pagina Batch size.
Altri
- Ottimizzazione basata su gradiente con momenti: Questi algoritmi introducono momenti o impulsi nella discesa del gradiente, consentendo un addestramento più veloce e stabile. Ad esempio, l’algoritmo del momento (Momentum) e l’ottimizzatore di Adam sono molto popolari.
- Ottimizzazione basata su gradiente con adattamento del tasso di apprendimento: Questi algoritmi regolano dinamicamente il tasso di apprendimento durante l’addestramento, permettendo una convergenza più rapida e stabile. Alcuni esempi noti includono l’Adadelta e l’Adagrad.
- Ottimizzazione basata su gradiente con normalizzazione del gradiente: Alcuni algoritmi incorporano tecniche di normalizzazione dei gradienti per evitare problemi di esplosione o scomparsa del gradiente. L’ottimizzatore di RMSprop è un esempio di questa categoria.
- Ottimizzazione basata su gradiente con regolarizzazione: Questi algoritmi combinano la discesa del gradiente con tecniche di regolarizzazione per prevenire l’overfitting. Un esempio è l’ottimizzatore L-BFGS, che utilizza la regolarizzazione L-BFGS.
- Ottimizzazione basata su popolazione: Questa categoria include algoritmi evolutivi che simulano il processo di selezione naturale per ottimizzare i parametri del modello. Gli algoritmi genetici sono un esempio noto di ottimizzazione basata su popolazione.
- Ottimizzazione basata su metodi di seconda derivata: Questi algoritmi utilizzano informazioni sulla seconda derivata della funzione di perdita per determinare la direzione e la dimensione degli aggiornamenti dei parametri. L’ottimizzatore di Newton-Raphson è un esempio di questa categoria.
Esempio
Supponiamo di avere un semplice problema di regressione lineare e vogliamo allenare un modello per adattarsi a un set di dati. Utilizzeremo Python e la libreria scikit-learn per illustrare come utilizzare due diversi algoritmi di ottimizzazione: la discesa del gradiente e l’ottimizzatore Adam.
#import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD, Adam
from sklearn.metrics import mean_squared_error
# Genera dati casuali per il problema di regressione
X, y = make_regression(n_samples=100, n_features=1, noise=0.1, random_state=42)
# Dividi i dati in set di allenamento e test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Crea un modello di regressione lineare con la discesa del gradiente
model_sgd = Sequential()
model_sgd.add(Dense(1, input_dim=1, activation='linear'))
model_sgd.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01)) # lr è il tasso di apprendimento
# Allenamento del modello con la discesa del gradiente
history_sgd = model_sgd.fit(X_train, y_train, epochs=100, verbose=0)
# Crea un modello di regressione lineare con l'ottimizzatore Adam
model_adam = Sequential()
model_adam.add(Dense(1, input_dim=1, activation='linear'))
model_adam.compile(loss='mean_squared_error', optimizer=Adam(lr=0.01))
# Allenamento del modello con l'ottimizzatore Adam
history_adam = model_adam.fit(X_train, y_train, epochs=100, verbose=0)
# Calcola le previsioni e l'errore quadratico medio per il modello con la discesa del gradiente
y_pred_sgd = model_sgd.predict(X_test)
mse_sgd = mean_squared_error(y_test, y_pred_sgd)
print(f"Errore quadratico medio utilizzando la discesa del gradiente: {mse_sgd}")
# Calcola le previsioni e l'errore quadratico medio per il modello con l'ottimizzatore Adam
y_pred_adam = model_adam.predict(X_test)
mse_adam = mean_squared_error(y_test, y_pred_adam)
print(f"Errore quadratico medio utilizzando l'ottimizzatore Adam: {mse_adam}")
# Visualizza i risultati
plt.scatter(X_test, y_test, label='Dati reali')
plt.plot(X_test, y_pred_sgd, color='red', label='Discesa del gradiente')
plt.plot(X_test, y_pred_adam, color='green', label='Adam')
plt.legend()
plt.show()
In questo esempio, abbiamo generato dati casuali per un problema di regressione lineare e diviso i dati in set di allenamento e test. Successivamente, abbiamo creato due modelli di regressione lineare utilizzando due diversi algoritmi di ottimizzazione: la discesa del gradiente e l’ottimizzatore Adam.
Il primo modello utilizza la discesa del gradiente per ottimizzare i parametri del modello e calcola le previsioni. Il secondo modello utilizza l’ottimizzatore Adam, che è noto per essere efficace nella maggior parte dei casi e regola automaticamente il tasso di apprendimento. Alla fine, calcoliamo l’errore quadratico medio (M
SE) per entrambi i modelli per valutare le loro prestazioni.
È importante notare che la scelta dell’algoritmo di ottimizzazione dipende dalla natura del problema e dalle sue specifiche esigenze. Mentre in questo esempio abbiamo utilizzato la regressione lineare, gli algoritmi di ottimizzazione sono ampiamente utilizzati in algoritmi più complessi come le reti neurali, il supporto vettoriale di macchine, l’apprendimento profondo e molte altre applicazioni di machine learning.
In sintesi, gli algoritmi di ottimizzazione nel machine learning svolgono un ruolo critico nell’addestramento dei modelli, aiutando a trovare i parametri ottimali che minimizzano la funzione di perdita. Esistono molte varianti di algoritmi di ottimizzazione, ognuna con le proprie caratteristiche e vantaggi. La scelta dell’algoritmo appropriato dipende dalla natura del problema e dalle esigenze specifiche, e spesso richiede un processo di sperimentazione e messa a punto per ottenere i migliori risultati.