La regressione è la previsione di un valore numerico target a partire da una serie di variabili di input (features).
I modelli di regressione cercano di stabilire una relazione matematica tra le variabili indipendenti e la variabile dipendente in modo da fare previsioni o stime.
Fa quindi una interpolazione con i dati in ingresso per fornire una funzione generica:
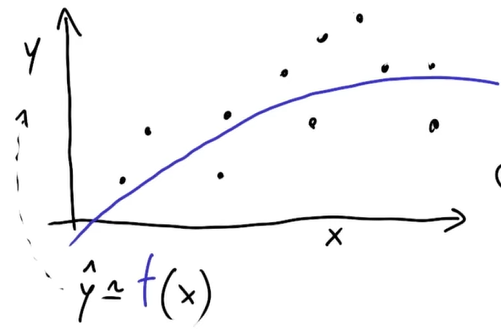
Ci sono diversi tipi di modelli di regressione, tra cui i principali sono:
- Regressione Lineare: La regressione lineare è uno dei modelli di regressione più semplici ed è utilizzata quando si presume che ci sia una relazione lineare tra le variabili indipendenti e la variabile dipendente. Il suo obiettivo è trovare la retta di miglior adattamento ai dati. Viene utilizzata per problemi di previsione o analisi di correlazione, ad esempio nel caso di previsioni dei prezzi delle case in base a variabili come dimensioni, posizione, ecc.
- Regressione logistica: La regressione logistica è utilizzata quando la variabile dipendente è binaria o categorica (due classi) e si desidera prevedere la probabilità di un'osservazione di appartenere a una delle due classi. È ampiamente utilizzata in problemi di classificazione binaria, come la predizione della probabilità di successo o insuccesso in base a variabili indipendenti.
- Regressione polinomiale: In questo tipo di regressione, si utilizzano equazioni polinomiali invece di una retta per adattare i dati. È utile quando i dati seguono una relazione non lineare. Ad esempio, si potrebbe utilizzare una regressione polinomiale per adattare una curva a un set di dati che segue una forma parabolica.
- Regressione non lineare: Questa categoria comprende una varietà di modelli che possono catturare relazioni non lineari tra variabili. Questi modelli possono includere funzioni non lineari, come sigmoidi o esponenziali, per adattare i dati in modo più flessibile.