Regressione logistica

La regressione logistica è classificatore in cui l'obiettivo è prevedere l'appartenenza di un'osservazione a una delle due classi possibili (ad esempio, “1” o “0”, “vero” o “falso”, “positivo” o “negativo”). Si chiama regressore anche se è un classificatore per motivi storici. Notate che, nonostante il suo nome, l’algoritmo a regressione logistica è un modello di classificazione e non di regressione. La regressione logistica si basa sulla funzione logistica (o sigmoide) per stimare la probabilità che un’osservazione appartenga a una delle due classi. Questa probabilità viene quindi mappata a una classe utilizzando una soglia di decisione (ad esempio, 0.5).

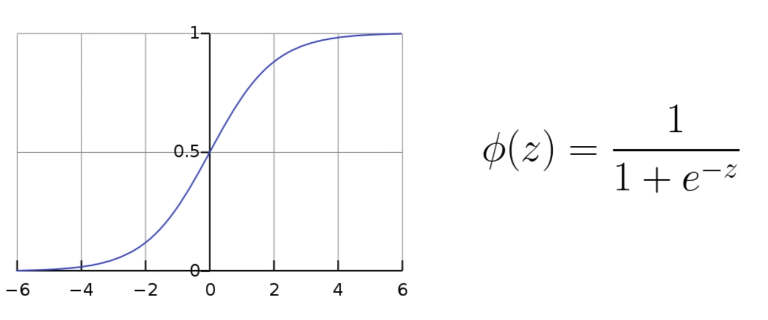
La formula matematica della regressione logistica è la seguente:

$P(Y=1|X)=\frac{1}{1+e^{-({\beta }_0+{\beta }_{1}X)}}$

Dove: -$P(Y=1|X)$ rappresenta la probabilità condizionata che $Y$ sia uguale a 1 dato $X$. -$X$ è la variabile indipendente. -${\beta }_0$ è l’intercetta. -${\beta }_1$ è il coefficiente associato a $X$. -$e$ è la base del logaritmo naturale.

Ecco uno script commentato in Keras per addestrare un modello di regressione logistica su un dataset di classificazione binaria:

from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
import numpy as np
 
# Genera dati di esempio per la classificazione binaria
X = np.random.rand(100, 1)  # Variabile indipendente
y = (X > 0.5).astype(int)  # Variabile dipendente binaria
 
# Crea un modello sequenziale per la regressione logistica
model = Sequential()
model.add(Dense(1, input_dim=1, activation='sigmoid'))  # Usiamo la funzione di attivazione sigmoide
 
# Compila il modello utilizzando la funzione di perdita di entropia incrociata binaria
model.compile(loss='binary_crossentropy', optimizer=Adam(learning_rate=0.01), metrics=['accuracy'])
 
# Addestra il modello
model.fit(X, y, epochs=100, verbose=0)
 
# Effettua previsioni (probabilità)
predictions = model.predict(X)
 
# Effettua previsioni (classi) utilizzando una soglia di decisione (0.5)
predicted_classes = (predictions > 0.5).astype(int)
 
# Valuta l'accuratezza del modello
accuracy = (predicted_classes == y).mean()
print("Accuracy:", accuracy)

In questo esempio, il modello utilizza una singola variabile indipendente $X$ per prevedere la probabilità di appartenenza alla classe 1. La funzione di attivazione sigmoid viene utilizzata per mappare la probabilità tra 0 e 1. La funzione di perdita binary_crossentropy è utilizzata come funzione di costo. Dopo l’addestramento, le previsioni vengono effettuate sia come probabilità che come classi binarie utilizzando una soglia di decisione del 0.5, e l’accuratezza del modello viene calcolata.

Decision boundary

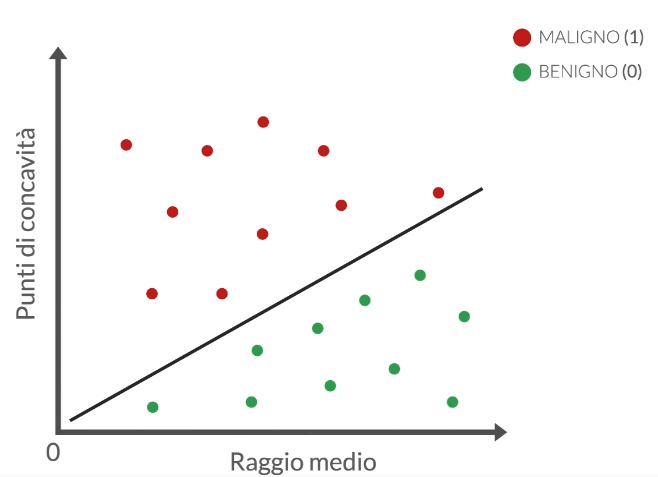
La “retta di decisione” (o “boundary di decisione”) nella regressione logistica è una linea immaginaria che separa due classi in un problema di classificazione binaria. La retta di decisione rappresenta il punto in cui la probabilità stimata dal modello di appartenenza a una delle due classi passa da una classe all’altra. In altre parole, è il confine tra le regioni in cui il modello classifica le osservazioni come “classe positiva” o “classe negativa”.

La formula matematica della retta di decisione nella regressione logistica può variare in base al numero di variabili indipendenti utilizzate nel modello. Per un problema di classificazione binaria con una singola variabile indipendente, la retta di decisione è una retta nella forma:

${\beta }_0+{\beta }_{1}X=0$

Dove:

• ${\beta }_0$ è l’intercetta del modello.
• ${\beta }_1$ è il coefficiente associato alla variabile indipendente $X$.

Nella notazione con bias (intercetta) e weight (coefficienti) l’equazione si può scrivere come

$\text{Bias}+{\text{Weight}}_1\cdot X_1+{\text{Weight}}_2\cdot X_2+\dots +{\text{Weight}}_n\cdot X_n=0$

Dove:

• $Bias$ è l’intercetta del modello, spesso denotata come ( \beta_0 ) nella notazione tradizionale.
• $Weigh{t}_i$ rappresenta il peso o il coefficiente associato alla variabile indipendente $X_i$.
• $X_i$ sono le variabili indipendenti (caratteristiche) del modello.

Questa retta divide lo spazio delle caratteristiche in due regioni, una in cui il modello predice la “classe positiva” (quando ${\beta }_0+{\beta }_{1}X>0$) e una in cui predice la “classe negativa” (quando ${\beta }_0+{\beta }_{1}X<0$).

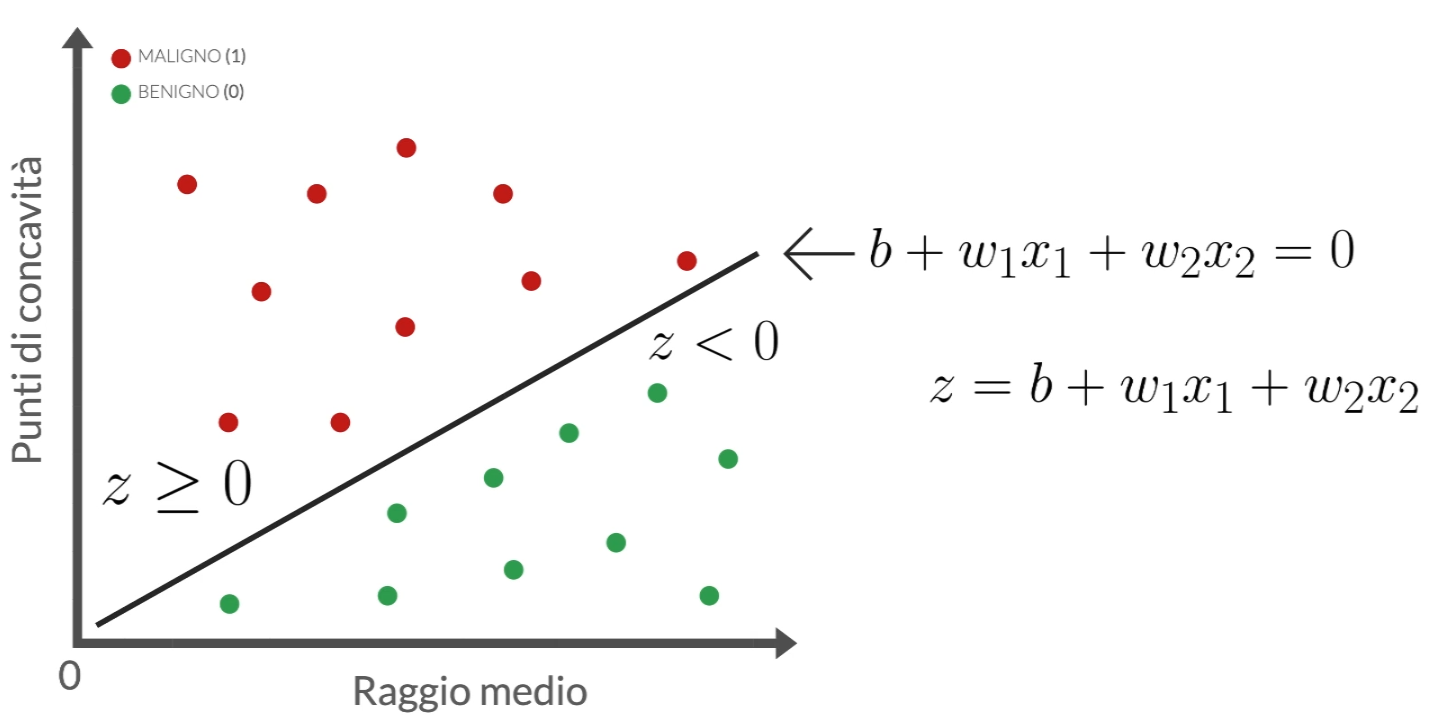
Tuttavia, se si hanno più di una variabile indipendente (un problema di classificazione multivariata), la retta di decisione diventa un iperpiano o una curva decisionale, a seconda della complessità del modello.

La retta di decisione è fondamentale per la capacità di classificazione del modello di regressione logistica, poiché determina come le diverse osservazioni vengono assegnate a una delle due classi. La scelta dei coefficienti ${\beta }_0$ e ${\beta }_1$ influenzerà la posizione e l’orientamento di questa retta di decisione.