Le tecniche di regolarizzazione nel machine learning sono metodi utilizzati per ridurre l’overfitting, un problema comune nelle tecniche di apprendimento automatico, in cui il modello si adatta troppo ai dati di addestramento e non generalizza bene ai dati non visti.
Ecco due delle tecniche di regolarizzazione più comuni:
- Ridge Regression (Regolarizzazione L2): In Ridge Regression, si aggiunge un termine di regolarizzazione alla funzione di costo durante l’addestramento del modello. Questo termine di regolarizzazione è proporzionale al quadrato della norma L2 dei coefficienti del modello. In pratica, questo significa che i coefficienti del modello sono costretti a rimanere piccoli. Ciò aiuta a evitare l’overfitting, specialmente quando ci sono molte variabili di input.
- Lasso Regression (Regolarizzazione L1): Simile alla Ridge Regression, ma utilizza la norma L1 dei coefficienti del modello invece della norma L2. Questo porta alla sparsità dei coefficienti, poiché tende ad annullare i coefficienti di alcune variabili meno importanti, riducendo così la complessità del modello. Questo rende Lasso Regression utile per la selezione delle feature, oltre alla riduzione dell’overfitting.
Entrambe queste tecniche introducono un termine di regolarizzazione che controlla la complessità del modello. Il parametro di regolarizzazione controlla quanto peso dare al termine di regolarizzazione rispetto al termine di costo della regressione. Aumentando questo parametro, si riduce la complessità del modello, il che può aiutare a ridurre l’overfitting.
In generale, le tecniche di regolarizzazione sono utili quando abbiamo un numero limitato di dati di addestramento rispetto al numero di variabili di input, o quando le variabili di input sono altamente correlate tra loro. Aiutano a prevenire l’overfitting regolarizzando i parametri del modello e riducendo la varianza, migliorando così le prestazioni del modello sui dati di test.
L1-L2
Un modo per trovare un buon compromesso fra bias e varianza e ridurre l'overfitting consiste nell’ottimizzare la complessità del modello tramite la regolarizzazione. Il concetto su cui si basa la regolarizzazione consiste nell’introdurre delle informazioni aggiuntive (bias), tipicamente alla funzione di costo, per penalizzare i pesi estremi del parametro. L’obiettivo è ridurre così la magnitudine dei pesi più grandi. La forma più comune di regolarizzazione è chiamata regolarizzazione L2 (chiamata anche riduzione L2 o decadimento dei pesi). Le funzioni di regolarizzazione si applicano ad ogni strato della rete, quindi io posso avere uno strato con L2 con parametro 0.01, un altro strano sempre con L2 a 1 e così via.
La L1 regularization (o “Lasso regularization”) aggiunge un termine alla funzione di costo equivalente alla somma assoluta dei valori dei pesi moltiplicati da una costante lambda. In pratica questo porta ad avere molti parametri vicini allo zero, ottenendo una sorta di selezione automatica delle feature più importanti: infatti i parametri con peso zero è come se non ci fossero nel modello, venendo così automaticamente esclusi, ho quindi una selezione delle proprietà.
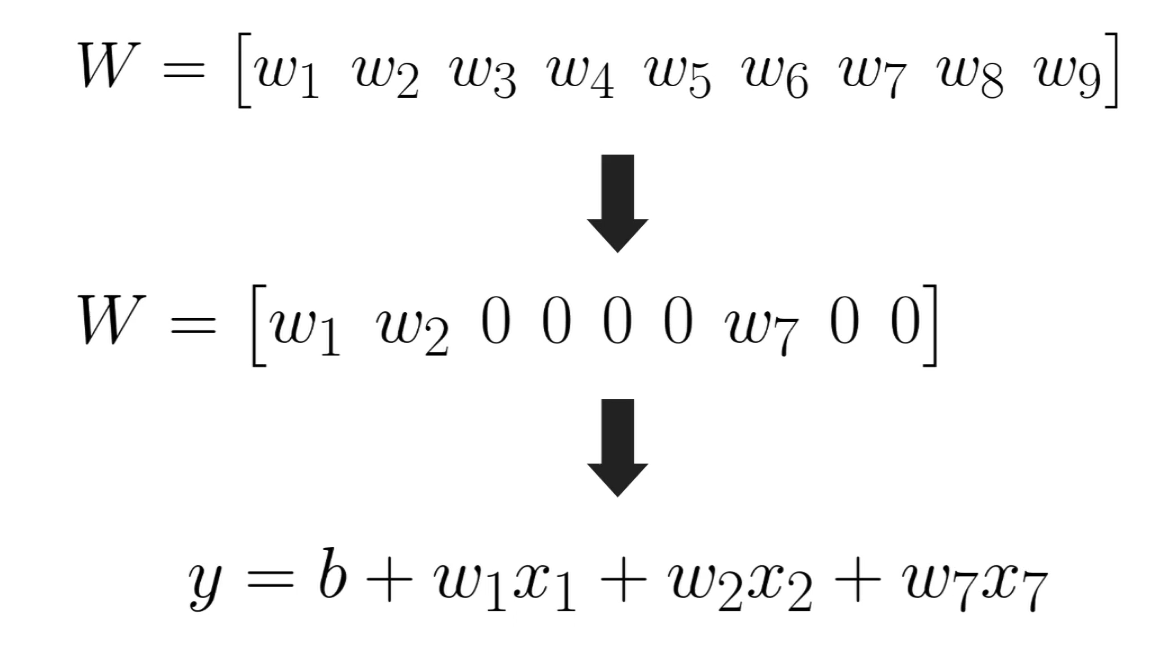
La L2 regularization (o “Ridge regularization”), invece, aggiunge un termine alla funzione di costo equivalente al quadrato della norma euclidea dei pesi moltiplicata da una costante lambda. In questo caso si cerca sempre di ridurre le dimensione dei coefficienti ma in modo meno aggressivo rispetto all’L1
Entrambe le tecniche cercano quindi di limitare la complessità del modello attraverso la penalizzazione sui grandi valori assunti dai parametri durante l’allenamento e possono essere usate anche contemporaneamente nella stessa rete neurale con diverso peso assegnato alle due regolarizzazioni.
In generale, se i dati sono rumorosi o non molto correlati tra loro è possibile che l’utilizzo della regolarizzazione possa migliorare le prestazioni del modello evitando overfitting; d’altra parte se i dati hanno già intrinsecamente poco rumore oppure se ci si vuole concentrare su dettagli specifici potrebbe essere meglio non applicarle per avere modelli più precisi ma complessivamente più grandi.
Dropout
Il dropout è un’altra tecnica di regolarizzazione specifica per il deep learning: invece di regolarizzare i pesi come fa L1-L2, il dropout regolarizza i neuroni durante l'addestramento eliminandone casualmente alcuni durante ogni iterazione dell'addestramento.
Il funzionamento del dropout è piuttosto semplice: durante l’addestramento, per ogni iterazione, i neuroni di un layer vengono disattivati con una probabilità prefissata, di solito compresa tra il 20% e il 50%. Ciò significa che i neuroni non contribuiscono alla fase di forward e Backpropagation in quella particolare iterazione. Di conseguenza, la rete deve imparare a fare affidamento su combinazioni diverse di neuroni per generare output, riducendo così la dipendenza da singoli neuroni o connessioni specifiche e migliorando la generalizzazione del modello. Il dropout funziona in quanto durante la fase di addestramento alcuni nodi tendono a farsi carico degli errori degli altri nodi (co-adaptation).
Durante la fase di test, tutti i neuroni vengono considerati attivi, ma i pesi dei neuroni sono scalati in modo che la somma delle attivazioni rimanga costante rispetto alla fase di addestramento. Questo aiuta a ottenere risultati coerenti tra l’addestramento e il test.
Il dropout è particolarmente efficace quando si lavora con reti neurali profonde, in quanto aiuta a prevenire l’overfitting e migliora la capacità di generalizzazione del modello. Inoltre, il dropout è relativamente semplice da implementare e può essere applicato a diverse architetture di reti neurali con poche modifiche.
Esempio
Ecco un esempio di come creare una rete neurale con 4 layer utilizzando Keras in Python, con regolarizzazioni L1 e L2 e dropout:
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras import regularizers
# Creazione del modello
model = Sequential()
# Aggiunta del primo layer con regolarizzazione L1 e dropout
model.add(Dense(64, input_shape=(input_shape,), activation='relu', kernel_regularizer=regularizers.l1_l2(l1=0.01, l2=0.01)))
model.add(Dropout(0.5))
# Aggiunta del secondo layer con regolarizzazione L1 e L2 e dropout
model.add(Dense(128, activation='relu', kernel_regularizer=regularizers.l1_l2(l1=0.01, l2=0.01)))
model.add(Dropout(0.5))
# Aggiunta del terzo layer con regolarizzazione L1 e L2 e dropout
model.add(Dense(64, activation='relu', kernel_regularizer=regularizers.l1_l2(l1=0.01, l2=0.01)))
model.add(Dropout(0.5))
# Aggiunta dell'ultimo layer di output
model.add(Dense(1, activation='sigmoid'))
# Compilazione del modello
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# Stampa della struttura del modello
model.summary()