Cambiando completamente argomento rispetto agli ultimi articoli sui cui mi sono soffermato principalmente su SQL Server, in questo post (parziale traduzione di quanto si può trovare nelle pagine http://homepages.inf.ed.ac.uk/rbf/HIPR2/morops.htm e seguenti) esporrò una breve introduzione agli operatori morfologici per l’elaborazione digitale di immagini indicandone i principali.
Lo studio della morfologia in matematica si dedica all’analisi di strutture geometriche comparando ogni pixel con i sui vicini in vari modi.
Gli operatori morfologici prendono in ingresso
- un’immagine binaria (o in scala di grigi)
- una matrice kernel
e li combinano utilizzando un insieme di operatori (intersezione, unione, esclusione, complementare).
Il kernel viene shiftato lungo l’immagine (convoluzione) in modo che ogni pixel dell’immagine sia confrontata con l’insieme dei pixel sovrapposti al kernel. Se due insiemi di elementi corrispondono alla condizione definita dall’operatore insiemistico, il pixel dell’immagine corrispondente al centro del kernel e impostato ad un valore predefinito (0 o 1 per le immagini binarie).
Conseguentemente possiamo dire che un operatore morfologico è definito da:
- il kernel
- l’operatore insiemistico
Per gli operatori morfologici base, il kernel contiene solo i pixel in foreground (per esempio 1), mentre gli altri non hanno importanza; tali operatori sono sempre una combinazione di erosion e dilation.
L’operatore morfologico più generale è l’hit and miss in quanto tutti gli latri operatori possono derivare da questo. Le sue varianti sono usate spesso per semplificare la rappresentazione degli oggetti in un’immagine binaria preservando allo stesso modo la loro struttura: per esempio prende lo skeleton di un oggetto e riordinare il risultato usando il thinning.
1.1 Immagini binarie
Un’immagine binaria è un’immagine i cui pixel assumono solo due possibili valori: 0 e 255. Spesso tali immagini sono create tramite un processo di thresholding di un’immagine in scala di grigi o colorata, in modo da separare correttamente l’oggetto dal suo sfondo.
Il colore dell’oggetto in questione (solitamente bianco) è detto foreground color. Il resto (solitamente nero) è detto invece background color.
In ogni caso la polarità dell’immagine può essere invertita in alcune situazioni, per cui l’oggetto è definito con 0 (nero) e il background con un valore diverso da 0.
1.1.1 Le immagini binarie negli operatori morfologici
Alcuni operatori morfologici assumono che vi sia una determinata polarità per poter procedere, conseguentemente se noi processiamo una immagine con polarità invertita, l’operatore avrà comportamento opposto. Per esempio se noi applichiamo un operatore closing ad un testo nero su background bianco, il testo subirà un’operazione di opening.
1.2 Immagini in scala di grigi
Un’immagine in scala di grigi è un’immagine i cui colori sono tutte sfumature del grigio. La ragione per differenziare tali immagini da tutte le altre immagini colorate è che ogni pixel contiene meno informazione. Infatti il colore grigio è il colore per cui le componenti rossa, verde e blu hanno tutte la stessa intensità (nello spazio RGB) e conseguentemente è necessario specificare solo un singolo valore di intensità per ogni pixel, invece che tre.
Solitamente tale valore è memorizzato in un intero a 8 bit, portando a 256 possibili sfumature diverse di grigio. Tali tipologie di immagini sono molto utilizzate nell’image processing in quanto sono sufficenti per poter eseguire la maggior parte dei task, riducendo notevolemente i tempi di computazione.
1.3 Kernel
Il kernel consiste in un pattern specificato da un numro di punti discreti relativo ad una determinata origine. Solitamente il kernel viene identificato come una matrice rettangolare 3x3 formata da 0 e 1 anche se applicazioni più compesse possono richiedere l’utilizzo di più valori diversi.
Viene definita sempre un’origine del kernel che non è necessario che corrisponda al centro dell’immagine, anche se spesso lo è.

La dilation è uno dei due operatori base (l’altro è l’erosion). L’effetto base è l’aumento graduale dei bordi delle regioni in primo piano (tipicamente i pixel bianchi di un’immagine binaria). Tali aree crescono in ampiezza e conseguentemente i buchi tra tali regioni diventano sempre più piccoli.
Il funzionamento avviene nel seguente modo: per ogni pixel in background, viene sovrapposto a questo il kernel con il centro di questo sopra il pixel che sto considerando. Se almeno un pixel nel kernel coincide con un pixel in primo piano (bianco), allora il pixel che sto considerando diventa anche lui bianco, quindi passa da background a foreground.
Usando come kernel una matrice 3x3 formata da tutti valori 1, l’effetto è che tutti i pixel in background che hanno un vicino un pixel in foreground diventano pixel di foreground.
E’ possibile usare anvche una matrice più grande per ottenere, in un solo passaggio, una più grande dilation, anche se, per ottenere lo stesso effetto, basta eseguire più ripetizioni della dilation con un kernel più piccolo.
La dilation è il reciproco dell’erosion, infatti eseguire una dilation dei pixel in foreground è analogo ad eseguire una erosion sui pixel in foreground
2.1 Applicazioni
2.1.1 Eliminazione rumore “salt and pepper”
Un esempio di uso della dilation è l’eliminazione di rumore “pepper noise”. Spesso però l’immagine originale, con il rumore rimosso, viene notevolemente degradata, in questi casi è consigliabile usare l’operatore di closing.
2.1.1.1 Il rumore “salt and pepper”
Uno dei rumori più comuni è il rumore detto “salt and pepper”. Il rumore in questo caso è dovuto ad errori di trasmissione, per cui i pixel corrotti sono settati al valore massimo o settati alternativamente al valore massimo e minimo.
Per questo tipo di rumore i normali filtri passa basso risultano inefficaci in quanto il valore dei pixel corrotti può variare notevolemente rispetto all’originale, conseguentemente la media (per esempi) può essere molto distante dal valore effettivo.
Per risolvere possono usarte un filtro mediano che elimina il rumore più efficacemente ed allo stesso tempo conserva meglio i bordi e i dettagli dell’immagine in modo migliore. Rimando ad un mio prossimo articolo sui filtraggi per una comprensione maggiore.
2.1.2 Edge detection
La dilation di può usare anche per l’edge detection, prendendo la dilation di un’immagine e poi sottraendo l’immagine orignale, il risultato ottenuto saranno solo i nuovi pixel inseriti dall’operazione, che saranno gli edge dell’immagine originale.
2.1.3 Insieme ad altri operatori
La dilation è usata inoltre come base per altri oepratori morfologici, spesso insieme ad alcuni operatori logici

Come indicato nel capitolo precedente, l’erosion è il contrario della dilation, conseguentemente erode i bordi dei pixel in foreground, diminuendo così l’area dell’oggetto in primo piano ed aumentando ocnseguentemente l’area dello sfondo.
Il funzionamento è simmetrico rispetto alla dilation, nel senso che ho sempre la sovrapposizione del kernel all’immagine, ma il pixel considerato viene settato a 1 se e solo se tutti i pixel del kernel coincidono con pixel in foreground.
Usando un kernel 3x3, l’effetto che che vengono rimossi i pixel in foreground che non sono ocmpletamente circondati da altri pixel in foreground.
3.1 Applicazioni
Simmetricamente alla dilation, l’erosion può essere usata per rimuovere rumore “salt and pepper” (ma portando a distorsioni) ed eseguire un semplice edge detection. L’utilizzo invece più interessante dell’erosion è il seguente.
3.1.1 Separare oggetti
Un esempio classico dell’erosion è separare oggetti che si toccano parzialmente in un’immagine binaria, in modo poi da poterli contare utilizzando un algoritmo di labelling (per esempio).
Assumiamo per esempio di avere la seguente immagine

e il mio obiettivo è contare il numero di monete.
Il problema di utilizzare in qualsiasi algorimto per risolvere il problema è che gli oggetti si toccano rendendo tutto più difficile.
La situazione può essere notevolmente semplificata prima eseguendo una erosion nell’immagine (un risultato pulito come quello indicato sotto vi è perchè il kernel utilizzato non è quadrato ma circolare), ottenendo così

una volta ottenuta questa immagine è semplice eseguire il conteggio utilizzando un algoritmo di labelling.
Opening e closing sono due operatori morfologici molto imporanti, entrambi derivati dalla combinazione di erosion e dilation.
L’effetto di un opening è in qualche modo analogo all’erosion in quanto tende e rimuovere dei pixel in foregroung dai bordi delle regioni dei pixel in primo piano. La differenza con l’erosion è che è meno distruttivo, in quanto tende a preservare le regioni in foreground che hanno una forma similare al kernel eliminando tutti gli altri.
A livello pratico, un’opening è semplicemente un’operazinoe di erosion seguita da una di dilation (utilizzando sempre lo stesso kernel).
4.1 Separare oggetti
L’opening, come l’erosion, può essere usato efficamente per separare (al fine di contare) degli oggetti in una immgine binaria.
4.1.1 Rilevare cerchi
Consideriamo la seguente immagine binaria

Vogliamo separare i cerchi dalle linee, in modo che possano essere facilmente contati. Eseguire un opening con un kernel a disco (non quadrato) fornisce il seguente risultato

Come si può notare, anche se alcuni cerchi sono stati leggermente distorti, le linee sono scomparse, che era l’obiettivo che ci eravamo prefissati.
4.1.2 Rilevare linee orientate
In questo secondo esempio prendiamo la seguente immagine

Supponiamo di voler estrarre separatamente le linee verticali dalle linee orizzontali. Per poter eseguire questo task devo modificare il kernel in modo da renderlo asimmetrico:
- Per rilevare le linee verticali utilizzo un kernel 3x9
- Per rilevare le linee orizzontali utilizzo un kernel 9x3
I risultati sono i seguenti
4.1.3 Considerazioni
E’ importante notare come l’opening (analogamente all’erosion) è utile per separare oggetti con un orientamento noto.
Come si è notato dagli esempi sopra, l’operazione è utile per separare circonferenze (che non hanno orientamento) oppure linee verticali o orizzontali, ma questo è molto lontano da dire che l’opening può essere definito un riconoscitore universale di oggetti.
Per esempio, se assumiamo di usare un kernel molto lungo e sottile per rilevare una penna in un’immagine, tale kernel rileverà solo le penne con il suo stesso orientamento.
Se è necessario trovare delle penne nell’immagine, indipendentemente dall’orientamento, dovrei avere un kernel per ogni possibile direzione.
E’ inoltre importante sottolineare che i kernel potrebbero anche eliminare delle parti interessanti dell’immagine e mantenerne invece di non desiderati e che trovare il giuste equilibrio potrebbe essere difficile se non impossibile.

Closing è l’operatore reciproco di opening ed è l’analogo della dilation in quanto tende ad aumentare i bordi dei pixel in foreground ma è meno distruttivo. Il closing tende e preservare i pixel in background che hanno una struttura simile al kernel, eliminando tutte le altre.
Closing è un opening all’incontrario, ciè è una dilation seguita da una erosion, usando sempre lo stesso kernel.
5.1 Applicazioni
L’operazione di closing è usata comunemente per migliorare immagini binarie ottenute da un thresholding. Per esempio, assumiamo di avere la seguente immagine

Eseguiamo una binarizzazione ottenendo la seguente:

Come si può notare il threshold ha classificato alcune parti del telefono (che dovrebbero essere foreground) come background.
Effettuando un closing con un kernel circolare ottengo la seguente immagine, molto più pulita.

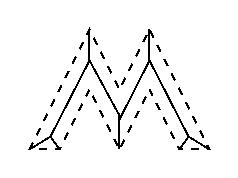
La skeletonization è il processo per cui i pixel in foreground vengono ridotti in uno “scheletro” che preserva l’estensione e la connettività dell’oggetto in foreground rappresentato ma eliminando buona parte di quest ultimo (solitamente lo skeleton è formato da linee di 1px).
Il modo più semplice di trovare lo skeleton di un immagine è eseguire un’operazione di thinning o erosion multipla fino a che non è più possibile.
Esistono numerosi algoritmi diversi per lo skeleton, ma i risultati che forniscono sono in qualche modo simili: non tutti però garantiscono che l’immagine ottenuta sia continua (anche se lo è l’oggetto originale).
6.1 Applicazioni
Lo skeleton è utile in quanto fornisce una semplice e compatta rappresentazione della forma dell’oggetto in questione. Per esempio può essere utile per calcolare la lunghezza di un oggetto calcolando la distanza tra i punti più distanti di uno skeleton.
Per esempio partendo da

lo skeleton corrispondente è

6.2 Sensibilità al rumore
L’operazione di skeleton è estremamente sensibile al rumore.
E’ assolutamente necessario eseguire delle operazioni per eliminare il rumore o le zone di discontinuità di un’immagine binaria (opening o closing per citare i più semplici) prima di eseguire lo skeleton, altrimenti questo risulta assolutamente inefficace.
Per esempio con la seguente immagine in ingresso

lo skeleton prodotto è il seguente