Una funzione di attivazione in una rete neurale è ciò che decide se un neurone particolare deve essere attivato o meno. In parole semplici, puoi immaginarla come un filtro che prende il segnale in entrata e decide se è abbastanza importante da essere passato al prossimo strato della rete.
Ecco alcune delle tipologie più comuni di funzioni di attivazione:
-
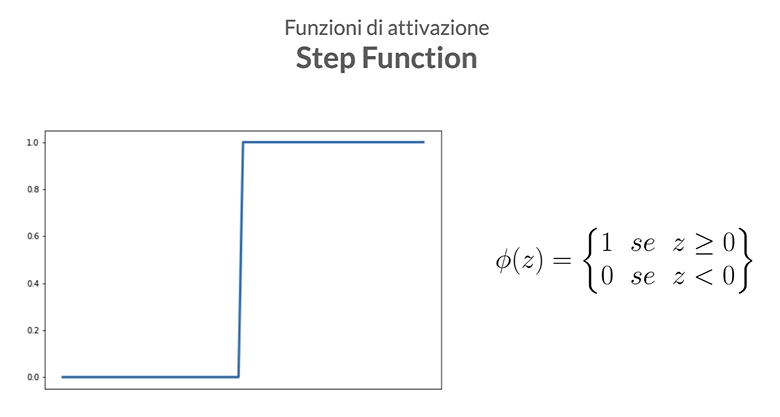
Step (o Funzione Gradino): Questa è forse la più semplice delle funzioni di attivazione. Funziona come un interruttore on/off. Se l’input è superiore a una certa soglia, il neurone viene attivato (emette un segnale, di solito 1), altrimenti resta inattivo (emette 0). Non è molto utilizzata nelle reti neurali moderne a causa della sua natura binaria e della mancanza di gradiente (non può essere utilizzata per metodi basati sul gradiente come la discesa stocastica del gradiente), ma è utile per comprendere le basi del funzionamento dei neuroni artificiali.
-
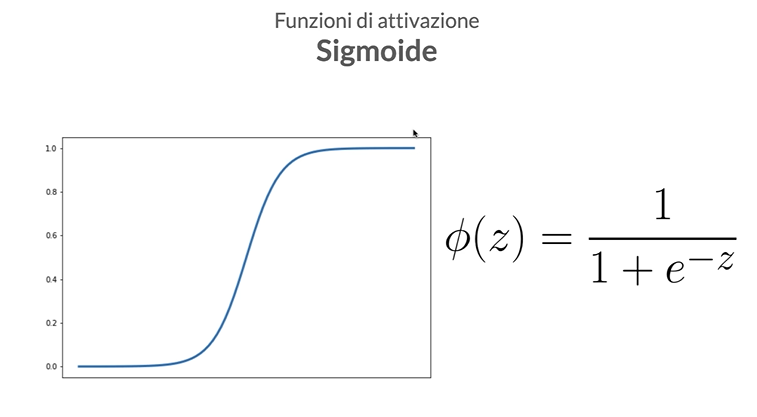
Sigmoid: Questa funzione trasforma i valori in entrata in un range tra 0 e 1. È utile per problemi di classificazione binaria. Tuttavia, non è molto usata oggi a causa di alcuni problemi come la scomparsa del gradiente.
-
ReLU (Rectified Linear Unit): È una delle funzioni più popolari. Trasforma tutti i valori negativi in zero e lascia invariati i valori positivi. È efficiente e generalmente funziona bene in molte applicazioni.

-
Leaky Relu: A differenza della ReLU standard, la Leaky ReLU consente ad una piccola quantità di informazione di passare anche quando l’input è negativo. La sua espressione matematica è:
dove è un piccolo valore positivo (generalmente nell’ordine di 0.01), noto come il parametro di “leakiness”.
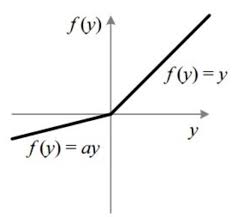
La Leaky ReLU è stata introdotta per superare il problema della “dying ReLU”, che si verifica quando i neuroni ReLU diventano inattivi durante l’addestramento e smettono di imparare completamente. L’aggiunta del termine “leaky” consente di mantenere il flusso di informazioni anche attraverso i neuroni con input negativi. In generale, può essere una scelta utile quando si vuole evitare la morte dei neuroni ReLU o quando si ha una quantità significativa di dati con valori negativi.
model = tf.keras.Sequential([
Input(shape=(input_size,)),
Dense(128),
LeakyReLU(alpha=0.01),
Dense(output_size, activation='softmax')
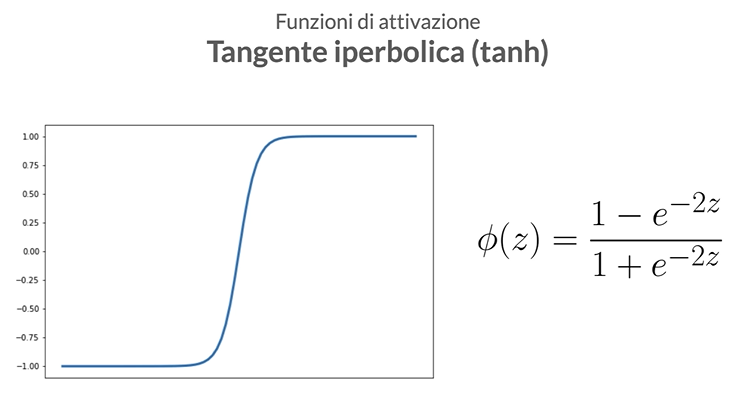
])- Tanh (Tangente Iperbolica): Trasforma i valori in un range tra -1 e 1. È simile alla sigmoid ma spesso funziona meglio perché i valori negativi possono essere gestiti in modo più efficace.
Quale funzione di attivazione utilizzare
Questa risposta non esiste e va ad esperienza ma una buona tecnica è usare una RELU per gli strati nascosti mentre per gli strati finali in base al problema che ho.
Classificazione monoclasse
In questo caso ho una classificazione semplice bianco/nero, esempio classico è tumore/non tumore. In questo caso avrò un solo neurone come livello di output che indica la probabilità che l’oggetto in ingresso sia quello ricercato e utilizzerò come funzione di attivazione la sigmoide.
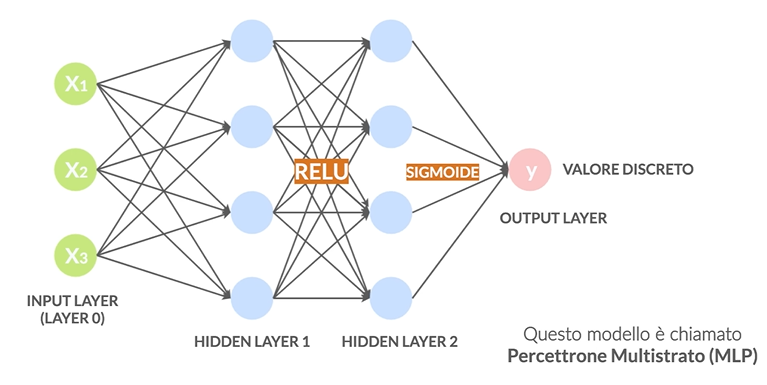
Classificazione con classi indipendenti
Se devo fare una classificazione di un oggetto in cui le classi di appartenenza sono indipendenti tra di loro, che significa che un’oggetto può appartenere sia alla classe 1 che alla classe 2 (es. se ricerco gli argomenti di un articolo di giornale, questo può trattare sia sport che attualità) allora utilizzo come funzione di attivazione la sigmoide. Ogni valore del nodi di output sarà tra 0 e 1 (in quanto utilizzo il sigmoide come funzione di attivazione dell’ultimo strato) e indica la probabilità che l’oggetto in ingresso appartenga alla classe
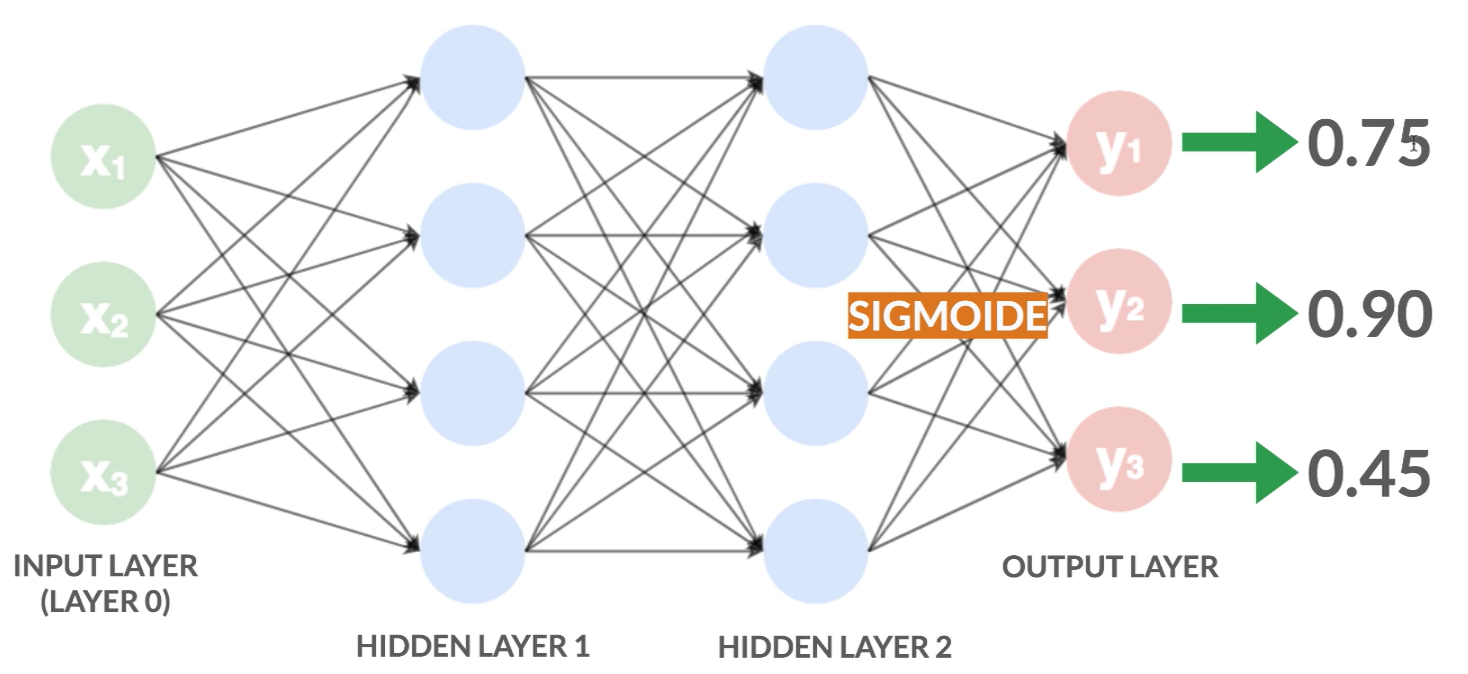 Nell’esempio sopra ottengo che l’oggetto in ingresso appartiene con il 75% di probabilità alla classe , con il 90% alla classe e con il 45% alla classe .
Notare che la somma di queste probabilità non fa 1, proprio perché l’oggetto può appartenere a più classi contemporaneamente.
Nell’esempio sopra ottengo che l’oggetto in ingresso appartiene con il 75% di probabilità alla classe , con il 90% alla classe e con il 45% alla classe .
Notare che la somma di queste probabilità non fa 1, proprio perché l’oggetto può appartenere a più classi contemporaneamente.
Classificazione con classi dipendenti
Questo è il caso più classico in cui un oggetto può appartenere solo ad una classe: per esempio se sto cercando la razza di un animale questo può essere “gatto” o “cane”, non può essere entrambi.
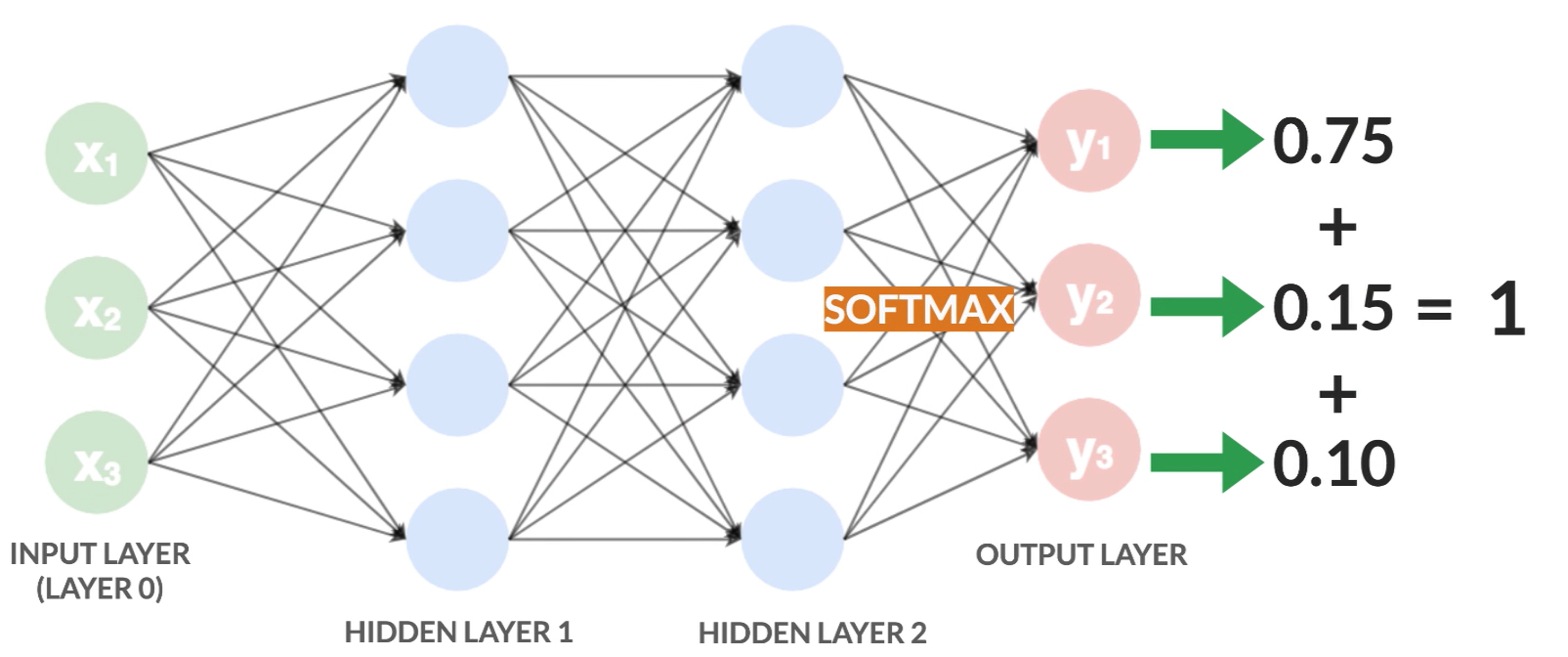
In questo caso utilizzo come funzione di attivazione dell'ultimo strato la softmax che fornisce sempre valori di probabilità tra 0 e 1 ma la cui somma totale fa 1.
In questo modo il nodo con la probabilità più alta è il nodo che indica la classe dell’oggetto di input.
Regressione
Se ho un problema di regressione e non classificazione utilizzo come funzione di attivazione la lineare.