Questo articolo è una parziale traduzione di quanto trovato in http://homepages.inf.ed.ac.uk/rbf/HIPR2/filtops.htm e nelle pagine correlate.
1. Introduzione
I filtraggi digitali di immagini sono usati principalmente per rimuovere le alte frequenza in un’immagine (come lo smoothing) o le basse frequenza (edge detection). Un’immagine può essere filtrata sia del dominio spaziale che nel dominio delle frequenze. Nel caso del filtraggio in frequenza, questo prevede prima il passaggio dell’immagine in tale dominio, l’applicazione del filtro ed infine la ritrasformazione nel dominio spaziale. Il filtro deve essere progettato in modo di attenuare alcune frequenze e salvare (o enfatizzare) altre. L’analogo nel tempo utilizza la convoluzione l’immagine col filtro.
2. Filtro medio (smoothing)
Questo tipo di filtro è il più semplice metodo per eseguire lo smoothing delle immagini, riducendo così la differenza tra l’intensità di un pixel e quella dei pixel ad esso adiacenti. Questa è l’implementazione più semplice di un filtro passa basso.
2.1 Funzionamento
Il filtro funziona semplicemente sostituendo il valore di ogni pixel con la media dei valori del vicinato, includendo se stesso. Così facendo si ha l’eliminazione dei valori di pixel che non sono rappresentativi rispetto al loro vicinato. Il filtro medio è il più semplice tra i filtri di convoluzione, in cui il kernel rappresenta la dimensione del vicinato. Solitamente è utilizzato un kernel 3x3, ma anche un kernel 5x5 può essere usato per avere una sfumatura più forte. Il kernel di questo filtro (nello spazio) è un rettangolo, conseguentemente, in frequenza, è un sinc.
2.2 Applicazioni
Il filtro medio è usato comunemente per ridurre il rumore di un’immagine. I problemi di usare questo metodo sono i seguenti:
- un singolo pixel con valori non rappresentativi per l’immagine può alterare la media di tutti i pixel nel suo vicinato
- Quando sono in corrispondenza di un bordo in un’immagine, il filtro eseguirà l’interpolazione con i pixel al di fuori del bordo ottenendo una notevole sfocatura di quest’ultimo.
Entrambi questi problemi sono risolti dal filtro mediano che vedremo nel capitolo seguente, che spesso è una soluzione migliore rispetto al filtro medio per ridurre il rumore, ma aumenta il tempo di computazione.
3. Filtro mediano
Analogamente al filtro medio, viene utilizzato per ridurre il rumore all’interno di un’immagine ma, a differenza di questo, fa un lavoro migliore preservando maggiormente i dettagli utili all’interno di quest’ultima.
3.1 Funzionamento
Come il filtro medio, il filtro mediamo considera ogni pixel nell’immagine e lo confronta con i vicini per decidere se un pixel è o non è rappresentativo. La differenza vi è sul fatto che, invece di eseguire una semplice sostituzione del valore del pixel con la media del vicinato, lo sostituisce con la valore mediano. Questo valore è calcolato prima ordinando i valori dei pixel in ordine crescente e in seguito eseguire una sostituzione del pixel con il pixel a metà della lista ordinata (se la lista è pari, eseguirò la media dei due valori centrali).
3.2 Applicazioni
Come il filtro medio, questo metodo è usato principalmente per ridurre il rumore, portando però i seguenti vantaggi:
- un pixel non rappresentativo non influenza il valore dei pixel del vicinato
- Dato che il valore di un pixel viene scelto uguale al valore di uno dei pixel del vicinato, non verrà mai creato un pixel con un valore non realistico, soprattutto in corrispondenza di un bordo. Questo filtro infatti preserva i bordi.
Il problema principale è che è relativamente complesso da computare. Per trovare il valore mediano è necessario ordinare la lista dei pixel del vicinato e questo è computazionalmente pesante, anche usando il quicksort.
4. Smoothing gaussiano
Lo smoothing gaussiano è un operatore di convoluzione per eseguire un “blur” dell’immagine rimuovendo allo stesso tempo dettaglio e rumore. In questo senso è simile al filtro medio, ma utilizza un kernel diverso, cioè una gaussiana.
4.1 Funzionamento
La distribuzione gaussiana è descritta dalla seguente formula
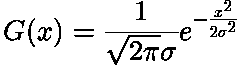
Dove gamma è la deviazione standard della distribuzione. Questa gaussiana ha media nulla, conseguentemente è centrata sullo zero. La forma è la seguente
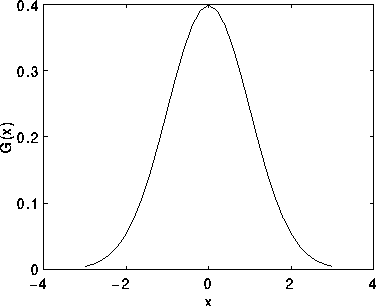
Un esempio di una tipico kernel gaussiano è il seguente
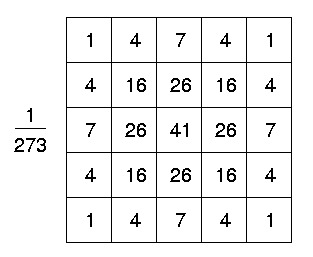
Una volte calcolato il kernel, il filtraggio avviene tramite convoluzione dell’immagine con questo kernel analogamente a quanto avviene con il filtro medio.
4.2 Applicazioni
L’effetto del filtro gaussiano è simile al filtro medio, con la differenza che la media non è una media “secca”, ma una media pesata che da più importanza al pixel centrale e sempre meno importanza mano a mano che mi allontano da questo. Per questo motivo questo metodo fornisce uno smooth migliore e preserva i bordi in maniera migliore. Uno dei motivi principali per usare questo tipo di filtro è la sua risposta in frequenza: molti filtri basati su convoluzione agiscono come filtri passa basso, ma l’analisi del kernel nelle frequenza mostra dei limiti. Abbiamo indicato qui sotto la rappresentazione, in frequenza, dei kernel di un filtro medio (rettangolo) e di un filtro gaussiano.
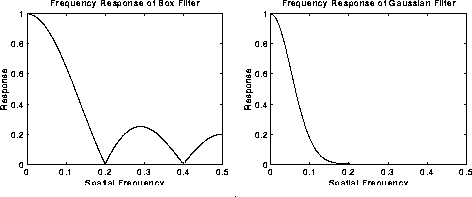
Come si può notare, la rappresentazione in frequenza del filtro medio è un sinc, mentre del filtro gaussiano è ancora un gaussiano. Entrambi agiscono come filtro passa basso ma, mentre il filtro gaussiano elimina completamente le frequenza alte, il sinc invece, per la sua natura oscillatoria, fornisce risultati meno attendibili. Un filtro gaussiano fornisce risultati certi sulle frequenze dell’immagine dopo il filtraggio, il filtro medio no. Questo risultato è utile per alcune tecniche di edge detection.
5. Smoothing conservativo
Lo smoothing conservativo è una tecnica di riduzione del rumore che, come dal nome “conservativo”, sacrifica la completa riduzione del rumore al fine di preservare i dettagli dell’immagine ad alta frequenza (sharp edges). E’ stato implementato in modo da ridurre i noise spikes (pixel isolati con frequenza molto alta o bassa) e non il rumore additivo (come il rumore gaussiano).
5.1 Funzionamento
Lo smoothing conservativo si assicura che l’intensità di ogni pixel sia limitata da un range di pixel definito dai suoi vicini. Per prima cosa quindi viene trovato il valore minimo e massimo di intensità tra tutti i pixel nel vicinato, se l’intensità del pixel centrale è all’interno di questo range allora non viene cambiato, altrimenti è settato al valore massimo (se maggiore) o minimo (se minore) del range.
5.2 Applicazioni
Questo filtro conserva maggiormente i bordi dell’immagine sia rispetto al filtro medio che mediano. Come scritto sopra, questo filtro funziona bene solo sul rumore impulsivo (salt and pepper) e non sul rumore additivo (rumore gaussiano).
6. Filtraggi in frequenza
I filtri in frequenza sono una categoria di filtraggi in cui l’applicazione del filtro avviene nel dominio delle frequenze e non nel dominio spaziale. L’immagine conseguentemente subisce una trasformazione di Fourier, viene moltiplicata con il filtro e poi ritrasformata nel dominio spaziale. Applicare un filtro passa basso fornisce uno smooth dell’immagine attenuando i bordi, un filtro passa alto invece gli enfatizza. Dato che la moltiplicazione in frequenza è la convoluzione nello spazio, teoricamente ogni filtro in frequenza può essere applicato anche nello spazio. In pratica invece, i filtri nello spazio spesso possono essere solo delle approssimazioni dei filtri in frequenza. Esistono tre diverse tipologie di filtro:
- Passabasso: attenua le alte frquenze rendendo i bordi più morbidi e diminueando il rumore;
- Passaalto: aumenta i bordi (utile per l’edge detection);
- Passabanda: migliora i bordi attenuando le basse frequenza riducendo allo stesso modo il rumore.
7. Filtro Laplaciano
Quiesto filtro viene utilizzato per enfatizzare le regioni di rapido cambiamento nei valori dei pixel e conseguentemente viene comunemente utilizzato per l’edge detection. Il laplaciano viene usato su immagini in scala di grigi che hanno subito prima uno smoothing (con un filtro gaussiano per esempio) al fine di ridurre la sua sensibilità al rumore.
7.1 Funzionamento
Il laplaciano di un’immagine I(x,y) è dato da
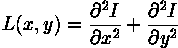
E questo può essere calcolato utilizzando la convoluzione. Due esempi di kernel comunemente usati che approssimano bene tale relazione sono i seguenti
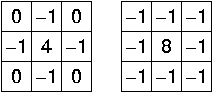
Dato che questi kernel sono un’approssimazione di una derivata seconda, sono molto sensibili al rumore. Per risolvere questo problema spesso sull’immagine in ingresso viene applicato un filtro gaussiano passa basso. E’ importante sottolineare che, dato che la convoluzione è un’operazione associativa, possiamo eseguire una convoluzione del filtro gaussiano con il filtro Laplaciano e poi convolvere questo filtro ibrido (chiamato filtro LoG) per l’immagine per ottenere il risultato desiderato. Usare questo metodo porta ai seguenti vantaggi:
- Visto che sia il kernel gaussiano che laplaciano sono molto più piccoli dell’immagine, questo metodo è molto più veloce della doppia convoluzione con l’immagine stessa
- Visto che il kernel LoG (Laplacian of Gaussian) può essere precalcolato in anticipo, solo una convoluzione deve essere eseguita in runtime sull’immagine
7.2 Applicazioni
L’operatore LoG effettua una derivata seconda sull’immagine, questo significa che nelle aree in cui l’immagine ha intensità costante il LoG sarà zero. Nelle vicinanze di un cambio di intensità la risposta LoG sarà positiva nella zona più scura e negativa nella zona più chiara. Conseguentemente considerando un bordo relativamente intenso che si pone tra due zone ad intensità costante ma diversa, la risposta LoG sarà:
- zero distante dal bordo;
- Positiva da un lato;
- Negativa dall’altro;
- Zero in qualche punto tra le due aree, o nello stesso bordo.
Per esempio con la seguente immagine in ingresso

Ottengo il seguente output

Eseguendo una combinazione lineare tra questo output e l’immagine in ingresso (per esempio in questo caso eseguendo un’addizione, ma in altri casi una sottrazione).